Ackermann/Works
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity

Add 'understanding-rsa.py'

Browse Source
This commit is contained in:
Ackermann 2023-02-05 19:00:41 +00:00
parent 2d13494c33
commit c240e54362
1 changed files with 254 additions and 0 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

254
understanding-rsa.py Normal file
View File

@ -0,0 +1,254 @@
# Understanding RSA
### Setting the Stage
I want this paper and exercise to be fun and enlightening for everyone.
I will try to make it fun and easy to follow along without glossing over too much of the underlying maths.<br>
That being said, if this is not for you, or you just hate math, I encourage you to still try.
I will be adding python code blocks you can run as we move through the paper which I hope will make it more interactive and engaging.
### So what is RSA?
We can't start talking about what RSA is without first paying homage to the creators, where it gets its name.<br>
Ron Rivest, Adi Shamir, and Leonard Adleman collaborated and invented this public key system back in 1977, which in of itself really
does show its stability since it is still used widely today. RSA as I said before is a public key system or also known as an
Asymmetric encryption. This basically means that the encryption key is actually made public for everyone to use, called a public keys
then a 2nd decryption key us held privately by the owner, simply named a private key.<br><br>
But I am sure many of you know this and thats not why you are here, you are here for the Juicy bits
### Defining the Language
As with most mathematics, someone a while ago decided to use fancy letters to represent things, probably as a way to flex their
intelligence... I'm joking for the most part, normally this is done to help differentiate between different types of mathematics.
I plan on doing some First order Logic papers eventually and you will see what I mean by that then.<br>
ANYWAY... Lets just make a table we can refer back to later to help.
|Symbol|Meaning|Do we Keep it Private?|
|---|---|---|
|p| Prime #1 | TRUE |
|q| Prime #2 | TRUE |
|n| n = p * q | FALSE |
|φ(n)| φ(n) = (p-1) * (p-1) | TRUE |
|e | pick any integer where 1 < e < φ(n) AND e is a coprime of (n AND φ(n))| FALSE |
|d | where d*e(mod φ(n)) = 1 | TRUE|
Now, I will gloss over the phi function here but if you want to learn more as to where it comes from there are links at the bottom<br>
e and d (for encryption and decryption) on the other hand needs some explaining but hang with me we have some tricks.
The first part of e is simple enough, we need a integer that is between 1 and φ(n) which at this point we know. The second part however,
what does coprime mean, well in this case it means it shares no common factors with both n and φ(n). Now what we can do to simplify this
is to just say e must be prime, and not a divisor of φ(n) (or if you divide φ(n) by e you do not get a whole number),
which we can do some quick checks to be sure.
For d what we need to find a value that results in multiplying it by e and then doing mod φ(n) which gives us 1. I will go into how to find
this in our first example.
To clear the air incase anyone is rusty or does not know what 'mod' means it basically is a remainder function, you shove
a number into a mod(n) and you get out what is left over. I like to picture it like a clock which is mod(12). So if you know
military time you kind of do this already, 1400 hours is actually 14 mod(12) which is 2, or 2pm. You count up to 12 and then
start back over so 5 mod(3) would be 2, and 12 mod(5) would be 2 like 1,2,3,4,5,1,2,3,4,5,1,2
### Example Please...
OK you stuck with me this long lets generate some keys. For this first one we will start with really small prime numbers.
Clearly this is a terrible idea since the smaller our starting primes are the easier it is to crack, but the math is still the same
and it is faster and easier to follow along.
1. Pick 2 primes, our p and q, let's say 67 and 79
2. Generate n by multiplying p and q to get 5293
3. Generate φ(n) by multiplying p-1 and q-1 to get 5148
4. For e, pick a prime number between 1 and 5148 and is not a divisor of 5148, let's go with 17
5. For d we find a value where d*e(mod φ(n)) = 1, lets go with 1817
OK, now you might be asking, how the hell did I get 1817 for d, the question feels kind of brute forced. Well this is where
I used the first bit of python code we really kind of need.
```py
def mvi(e,phi_n):
for x in range(1,phi_n):
if((e%phi_n)*(x%phi_n) % phi_n==1):
return x
```
I called this mvi which is short for Modular Multiplicative Inverse, which I will also kind of gloss over as well,
but I wanted you to see that you don't need to manually guess and check by hand, this does it for you.
So now we have our numbers, let't table them back out
|Symbol|Value|
|---|---|
|p| 67 |
|q| 79 |
|n| 5293 |
|φ(n)| 5148 |
|e | 17 |
|d | 1817 |
### Great now what...
Well now the fun starts, again we are kind of doing this by hand so rather than starting with a string and converting it
to a number to encrypt then send and then decrypt then convert back into a string lets just encrypt a number using our
new keys
First we need to send our Pub key to Alice, this is the pair of numbers e and n, so we will send her (17, 5293).
Again this is public, so we can send this however we like, as long as we are sure its not messed with on the way.
Now Alice will send us a secret number by encrypting a clear number using this public key and that is done with the
following function<br>
NOTE: For those that do not know, the power function in python (pow()) allows for 3 inputs with the 3rd being Mod which comes in really handy for us since it is way more effienent than doing `message**e % n`
```
def encrypt(message,e,n):
return pow(message,e,n)
```
Thats it, so in this case let's send 791, so we do `encrypt(791,17,5293)` which results in 5215
Bob gets 5215 and needs to decrypt it and that is done with this function
```
def decrypt(message,d,n):
return pow(message,d,n)
```
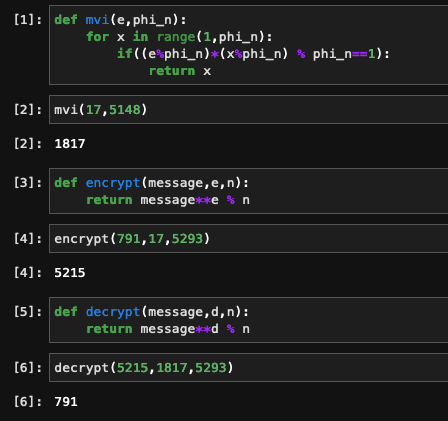
This is almost the same but we swap out the e for the d, and if we plug in `decrypt(5215,1817,5293)` we get, you guessed it, 791
And to show Im not making this up...
[![python.png](https://docs.hackliberty.org/uploads/images/gallery/2022-05/scaled-1680-/TqDpiF2ceumYtBO2-python.png)](https://docs.hackliberty.org/uploads/images/gallery/2022-05/TqDpiF2ceumYtBO2-python.png)
The last bit is a full python function you can play with to do some encrypton and decryption using what I have shown
```py
def simple_rsa_gen():
# Just a short list of 3 digit primes we can pick from so you dont need to find your own
primes = [211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,337,347,349,353,359,367,373,379]
# Lets pick our p and q from this list
p = primes[(randint(1,29)-1)]
q = primes[(randint(1,29)-1)]
# Lets make sure we did not happen to pick the same prime for both
if p == q:
while p == q:
q = primes[(randint(1,29)-1)]
print("p = "+str(p))
print("q = "+str(q))
# Now lets generate n by getting the product
n = p * q
print("n = "+str(n))
# Lets get that phi_n we need
phi_n = (p-1)*(q-1)
print("phi_n = "+str(phi_n))
# Lets find a good value for e, remember this needs to be a prime between 1 and phi_n and cannot be a divisor of phi_n
# you will see my range is not going to start at 1, first becuase 1 is not prime also I want to move into 3 digits to start
def get_e(var_phi_n):
for i in range(101, var_phi_n):
prime = 1
for j in range(2, i // 2 + 1):
if (i % j == 0):
prime = 0
break
if (prime == 1):
if var_phi_n % i != 0:
return i
break
# So let me break down what I just did, first we need to pass in what out phi_n is, that will be out upper limit
# then we need to determine if its a prime which we can do by seeing if its mod returns 0 for any int up to itself
# which in laymans terms means does it have any devisors at all, then if it is a prime we just make sure it't not
# a divisor of phi_n which just can be checked with does phi_n mod n = 0, if it does its no good
# Now we are starting at 101 and in most cases this will work for us, would be rare to find an instance where 101
# is infact a divisor of your phi_n so expect to see it more times than not. In general the goto e is actually 2^16 + 1 = 65537
e = get_e(phi_n)
print("e = "+str(e))
# Lets get that d value we need, the bigger phi_n gets the longer this could take
# here we are doing that mvi funtion again and the larger your starting primes the longer this can take
def mvi(var_e,var_phi_n):
for x in range(1,phi_n):
if((var_e%var_phi_n)*(x%var_phi_n) % var_phi_n==1):
return x
d = mvi(e, phi_n)
print("d = "+str(d))
# Now we have all of he numbers we need. Lets make our pub and priv keys and end this.
print("Your Public key is ("+str(e)+","+str(n)+")")
print("Your Private key is ("+str(d)+","+str(n)+")")
# Now we can use these with the encrypt and decrypt functions we made before
```
The output from above will look something like this
```
p = 283
q = 211
n = 59713
phi_n = 59220
e = 101
d = 57461
Your Public key is (101,59713)
Your Private key is (57461,59713)
```
And then you can use them to run those functions we defined before
[![encdec.png](https://docs.hackliberty.org/uploads/images/gallery/2022-05/scaled-1680-/q7YOjVDrTov5Cuw6-encdec.png)](https://docs.hackliberty.org/uploads/images/gallery/2022-05/q7YOjVDrTov5Cuw6-encdec.png)
### Is this real life?
For the most part yes, of course it is. The big differences are when actually implemented in code there are some better
methods for being more efferent as well as using random primes that are hundred of digits long, not 2.
For example, try the above code and method with 2 much bigger Mersenne primes 2^521 - 1 and 2^607 -1
You can see this in practice in the openssl sourcecode for rsa generation here.<br>
[OpenSSL rsa_gen.c](https://github.com/openssl/openssl/blob/master/crypto/rsa/rsa_gen.c)<br>
Look around line 174 and go from there, see if you can gather what its doing and how it is being more efficient than what we did.
### So you seen some stuff
This was a very high level and I did for sure gloss over some things but the math is there and I encourage you to look at
what I have shown here and ask yourself some questions, challenge yourself
1. Can you see any potential issues, how would you get past them?
2. Can you update the functions to use strings not just numbers?
3. In our first example what happens if I picked the number 31337 like we did in the 2nd example?
If you liked this please let me know back in the community post where I linked this, if you have questions or want more
let me know that too.
### More Links
I said I would
- https://en.wikipedia.org/wiki/RSA_(cryptosystem)
- https://en.wikipedia.org/wiki/Modular_multiplicative_inverse
- https://yewtu.be/watch?v=-ShwJqAalOk
- https://yewtu.be/watch?v=JD72Ry60eP4
- https://yewtu.be/watch?v=S9JGmA5_unY
- https://yewtu.be/watch?v=O4xNJsjtN6E
### A Little More
When I changed to pow(message,d,n) I was able to do bigger primes much faster so I put together another one using 5 digit primes you can play with.
```py
def bigger_rsa_gen():
# Doing a bit Bigger list of 5 digit primes now
# I stripped comments to save space
primes = [17029,17033,17041,17047,17053,17077,17093,17099,17107,17117,17683,17707,17713,17729,17737,17747,17749,17761,18233,18251,18253,18257,18269,18287,18289,18301,18307,18311,18313,18329,18341,18353,18367,19207,19211,19213,19219,19231,19237,19249,19259,19267,19273,19289,19301,19309,19319,19333,19373]
p = primes[(randint(1,49)-1)]
q = primes[(randint(1,49)-1)]
if p == q:
while p == q:
q = primes[(randint(1,49)-1)]
print("p = "+str(p))
print("q = "+str(q))
n = p * q
print("n = "+str(n))
phi_n = (p-1)*(q-1)
print("phi_n = "+str(phi_n))
def get_e(var_phi_n):
for i in range(10007, var_phi_n):
prime = 1
for j in range(2, i // 2 + 1):
if (i % j == 0):
prime = 0
break
if (prime == 1):
if var_phi_n % i != 0:
return i
break
e = get_e(phi_n)
print("e = "+str(e))
def mvi(var_e,var_phi_n):
for x in range(1,phi_n):
if((var_e%var_phi_n)*(x%var_phi_n) % var_phi_n==1):
return x
d = mvi(e, phi_n)
print("d = "+str(d))
print("Your Public key is ("+str(e)+","+str(n)+")")
print("Your Private key is ("+str(d)+","+str(n)+")")
```